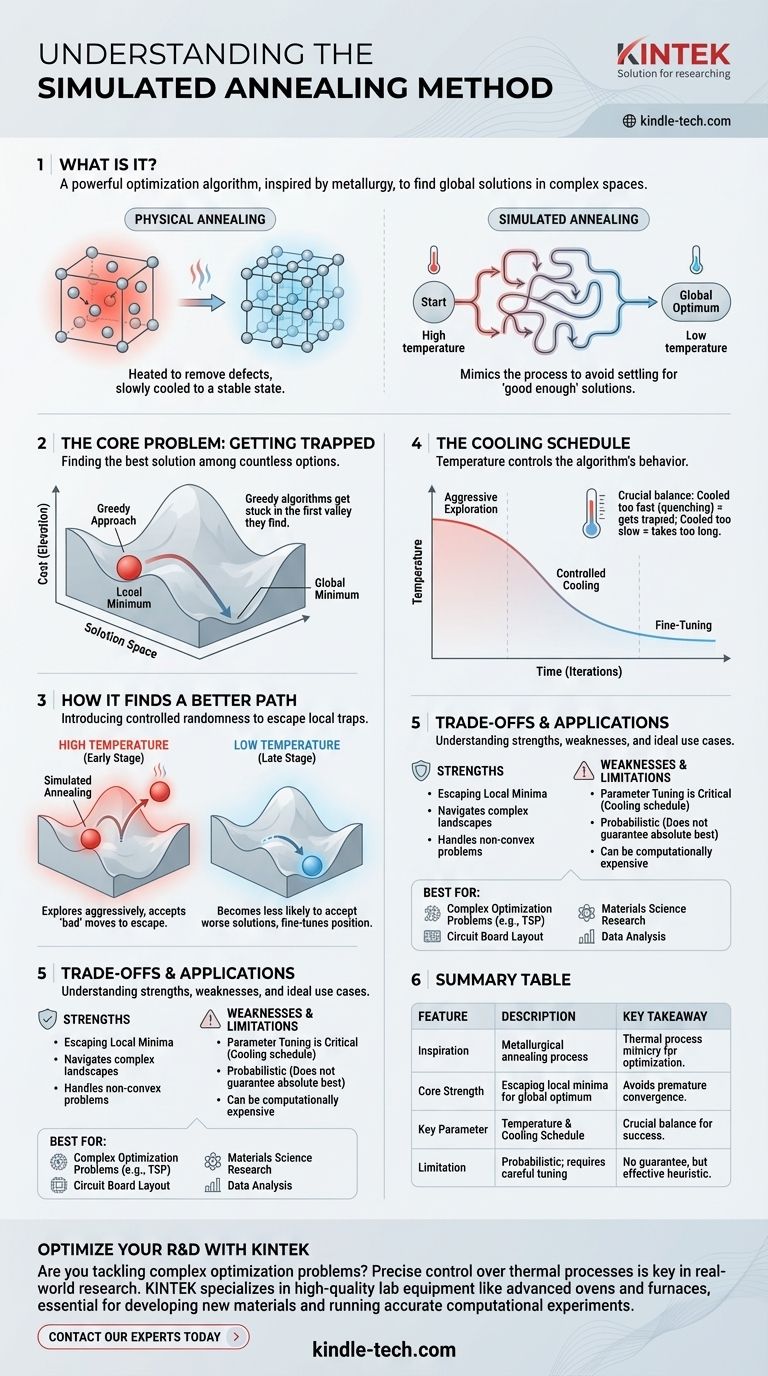
簡単に言うと、焼きなまし法(Simulated Annealing)は、広大で複雑な探索空間において、優れた(そしてしばしば大域的な)解を見つけるために使用される強力な最適化アルゴリズムです。これは、材料を加熱し、その後ゆっくりと冷却して欠陥を取り除き、安定した低エネルギーの結晶状態に到達させる冶金学的な焼きなましプロセスに直接着想を得ています。このアルゴリズムは、この物理プロセスを模倣して抽象的な計算問題を解決します。
焼きなまし法の核心は、金属の焼きなましという物理プロセスを模倣することで、「十分良い」解で満足してしまうという一般的な落とし穴を回避することです。まず、幅広い可能性を探索し(高温)、徐々に焦点を絞って高品質で安定した解へと導きます(低温)。

核心的な問題:トラップされること
焼きなまし法を理解するためには、まずそれが解決する問題、つまり無数の選択肢の中から可能な限り最良の解を見つけるという最適化のタスクを理解する必要があります。
解のランドスケープ
問題に対するすべての可能な解が、広大な起伏のある地形上の点であると想像してください。各点の標高は「コスト」を表し、標高が低いほど良い解です。あなたの目標は、マップ全体の最も低い点、つまり大域的最小値を見つけることです。
「貪欲な」アプローチとその欠陥
丘登り法と呼ばれる単純なアルゴリズムは、ランダムな点から開始し、常に下り坂に移動します。これは即座に改善をもたらす移動のみを受け入れるため、「貪欲な」アプローチです。
問題は、この方法が最初に見つけた谷、つまり局所的最小値で立ち往生してしまうことです。次の丘の向こうに、はるかに深い谷、つまり大域的最小値が存在するかどうかを知る術がありません。
焼きなまし法がより良い経路を見つける方法
焼きなまし法は、制御されたランダム性の要素を導入することで、これらの局所的なトラップから脱出することを可能にし、この制限を克服します。
インスピレーション:物理的な焼きなまし
冶金学では、金属を加熱することで原子に十分なエネルギーが与えられ、自由に動き回り、最適ではない欠陥のある構造から抜け出します。金属がゆっくりと冷却されるにつれて、原子は非常に秩序だった強力な結晶格子、つまり最小エネルギーの状態に落ち着く時間を得ます。
アルゴリズム:制御ノブとしての温度
焼きなまし法は、温度パラメータを導入することでこの概念を採用しています。これは物理的な温度ではなく、アルゴリズムの挙動を制御する変数です。
アルゴリズムは高温から開始します。この状態では、熱い金属中の活発な原子のように、解のランドスケープを積極的に探索します。現在の位置よりも悪い移動を受け入れる確率が高くなります。これが鍵です。「悪い」移動をすることが、局所的最小値から抜け出すことを可能にするのです。
冷却スケジュール
アルゴリズムが実行されるにつれて、冷却スケジュールに従って温度が徐々に下げられます。温度が低下するにつれて、アルゴリズムは悪い解を受け入れる可能性がますます低くなります。
最終的に、非常に低い温度では、アルゴリズムは単純な丘登り法のように振る舞い、改善のみを受け入れ、おそらく大域的最小値である位置を微調整します。
トレードオフの理解
他の強力なツールと同様に、焼きなまし法も万能な解決策ではありません。その限界を理解することは、効果的に使用するために不可欠です。
強み:局所的最小値からの脱出
その主な利点は、多くの局所的最小値を持つ複雑で非凸なランドスケープをナビゲートする能力です。貪欲なアルゴリズムが常に失敗する問題に対して、焼きなまし法は優れた選択肢です。
弱点:パラメータ調整が重要
アルゴリズムの性能は、冷却スケジュールに非常に敏感です。冷却が速すぎると、いずれにしても局所的最小値にトラップされる可能性があります(「急冷」)。冷却が遅すぎると、解を見つけるのに非現実的な時間がかかる可能性があります。適切なスケジュールを見つけるには、多くの場合、実験が必要です。
限界:確率的な方法であること
焼きなまし法は、絶対的な最良の解(大域的最小値)を見つけることを保証するものではありません。これはヒューリスティックであり、合理的な時間内に非常に良い解を見つけるように設計されています。常に、最適ではない状態に落ち着く統計的な可能性があります。
問題に適した選択をする
このガイダンスを使用して、焼きなまし法が最適化タスクに適したアプローチであるかどうかを判断してください。
- 多くのトラップ(局所的最小値)を持つ複雑な問題を解決することが主な焦点である場合:焼きなまし法は、特に巡回セールスマン問題や回路基板のレイアウトなどの古典的な問題にとって、最適なツールの1つです。
- 最大の速度で証明可能な最適解を見つけることが主な焦点である場合:線形計画法や標準的な貪欲なアプローチのような、より高速で決定論的なアルゴリズムで解決できるほど問題が十分に単純であるかどうかを最初に確認する必要があります。
最終的に、焼きなまし法は、より単純な方法では失敗するような、広大で困難な探索空間をナビゲートして高品質な解を見つけるための堅牢なフレームワークを提供します。
要約表:
| 特徴 | 説明 |
|---|---|
| 着想源 | 冶金学的な焼きなましプロセス(加熱と徐冷) |
| 核となる強み | 局所的最小値から脱出し、大域的最適解を見つける |
| 主要パラメータ | 温度と冷却スケジュール |
| 最適用途 | 多くの局所的なトラップを持つ複雑な最適化問題 |
| 限界 | 確率的;慎重なパラメータ調整が必要 |
KINTEKで研究開発を最適化
材料科学、化学工学、データ分析における複雑な最適化問題に取り組んでいますか?焼きなまし法の原理は、現実世界の熱プロセスから着想を得ており、研究室でこれらのプロセスを正確に制御することが重要です。
KINTEKは、研究開発に不可欠な均一な加熱と制御された冷却を提供する高度なオーブンや炉を含む、高品質の実験装置を専門としています。新しい材料を開発している場合でも、計算実験を行っている場合でも、信頼性の高い装置は正確な結果の基盤となります。
今すぐ専門家にお問い合わせください。最適化ワークフローを強化し、画期的な結果を達成するための完璧な実験室ソリューションを見つけましょう。
ビジュアルガイド